Difference between revisions of "Multiple constraints"

Revision as of 14:12, 27 March 2007

Description

This article discusses issues which arise with multiple constrained type parameters.

Formal generic type parameters with multiple constraints

The new ECMA standard for Eiffel introduces multi-constraint formal generic type parameters.

class C [G -> {A, B}]
end

Class C expects a type parameter that conforms to A and B. To make the text a bit easier to read I sometimes abbreviate the term 'formal generic type parameter' simply as 'formal'. So "G is the only formal of class C" means that G is the only formal generic type parameter of class C.

Qualified calls

Explanation of the issue

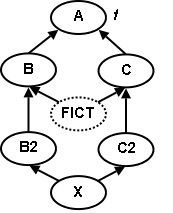
Consider this example inheritance hierarchy together with the following code:

Example: class GENERIC_CLASS [G -> {B, C}]   feature   g: G   example is do g.f -- qualified feature call end   end

Our interest is focused on the qualified feature call g.f of the example feature. With the dynamic binding semantics defined in section 8.16.11 of the ECMA standard, it makes a difference whether the static type of g is A, B or C. An illustration of the differences can be found in the Transposition article.

The standard defines in section 8.12.23 what the base type of such a multiple constrained formal type parameter is. It is a fictitious class (denoted as a dashed class FICT in the diagram) which inherits from all constraint classes and to which a possible renaming is applied. Dynamic binding requires a clear notion of what the static type of a target (here g) is. To obtain the correct feature, one needs the static and dynamic type of the target at runtime. Normally the base type of the target is taken as the static type. But we cannot take this fictitious base type as our static type, because, as can be seen in the diagram, it is outside of the conformance paths to X and therefore not usable with the current definition of dynamic binding.

The definition of this fictitious type FICT can only be used to clearly define the set of available features to instances of type G. It can not be used to define the semantic of a qualified feature call (like f.a).

To be able to use the type G one must provide a clear definition which static type is to use for a qualified feature call. An ambiguous feature, regarding the dynamic binding problematic, is a feature which is inherited through multiple constraining types. In our example this is the case for the feature f. It occurs in B and in C.

Solution proposal: Common Ancestor

If we have a multi-constraint formal type parameter and a qualified feature call on a target of that type, we define the static type to be the type of the class which introduced the current version of the called feature body. This must be a common ancestor of the constraining class types which contain the feature f (in our case B and C).

In our example we would set the static type of f to A and then execute the qualified feature call.

Properties of this solution:

• All features can be directly called on a target of type G.

• The static type of g may change depending on which feature is called.

Solution proposal: Manual Static Type Selection

The basic idea is to disallow ambiguous qualified calls on targets of type G at all. In our example it would not be valid to do the call g.f because the feature f is ambiguous as it is inherited over multiple paths (once through B and once through C).

As a consequence the programmer needs to resolve ambiguities manually. He does that by using either

• explicit renaming
• local variables
• object test

Using explicit renaming:

class GENERIC_CLASS [G -> {B rename f as f_b end, C rename f as f_c end}]
 
feature
 
   g: G
 
   example is
      do       
         g.f_b   -- qualified feature call with static type B
         g.f_c   -- qualified feature call with static type C
      end
 
end

The programmer resolves the issue by renaming in the first place.

Using a local variable:

example is
      local
         b: B
      do 
         b := g
         b.f      -- qualified feature call with static type B
      end

The programmer explicitly choses static type B by assigning g to the local variable b.

Using the object test:

example is
      do 
         check {bg: B | g } end
         bg.f  -- qualified feature call with static type B
      end

In this version the static type is chosen due to an object test.

Properties of this solution:

• Not all feature calls can be applied to a target whose type is a multi-constraint generic.

• The definition of the static type of every call remains straight forward.

Option

The renaming clause for multi-constraint types could be removed and name clashes could be regarded as ambiguous cases too. The user resolves it as shown above by choosing a static type explicitly over locals and object tests only.

Abstract creation

Formal generic type parameters in constraints

Introduction

As a special case of a constraint a formal is allowed:

class C [G -> {H, A}, H -> {A, B}]
end

Recursive definitions are allowed too and explicitly mentioned in the standard:

class C [G -> {H, A}, H -> {A, B, G}]
end

Renaming Issues

The question is now, how the renaming is handled for formal generic types.

• One could use the base type and apply a further renaming to it.
• One disallows renaming on formals.

Solution proposal: Base Type

As previously stated the base type of a multi-constraint formal is defined in section 8.12.23: Base type of a multi-constraint formal generic type and it can be used to define which features are available to the formal.

class C [G -> {H rename is_eq_a as is_eq_h_a end,
               A rename is_eq as is_eq_a},
         H -> {A rename is_eq as is_eq_a end,
               B}]
end

This approach however can become more complex if you consider it in the context of a set of formals which include a recursion in their definition:

class C [G -> H rename is_equal as is_equal_of_h end,
         H -> G rename is_equal_of_h as is_equal end]
feature
   f
      local
         l_g: G
         l_h: H
      do
         l_g.is_equal_of_h (l_h)
         l_h.is_equal (l_g)
      end
end

The base types of G and H look according to the definition something like this:

class FICT_BASE_TYPE_OF_G
inherit
   H
      rename is_equal as is_equal_of_h end
end
 
class FICT_BASE_TYPE_OF_H
inherit
   G
      rename is_equal_of_h as is_equal end
end

All the other conflicts (feature name clashes) which occur are resolved through renaming as well according to the definition. This renaming is however not accessible by the developer and omitted in the example.

What is noteworthy for this example is:

• A formal occurs directly in the inheritance part.
• There is a cycle in the inheritance hierarchy.

Both of them are not allowed in proper Eiffel code.

Solution proposal: No Renaming on Formals

This forces the developer to rename each feature he wants to use once properly to it's final name.

class C [G -> {H,
               A rename is_eq as is_eq_g_a end},
         H -> {A rename is_eq as is_eq_h_a end,
               B rename is_eq as is_eq_b_a end}]
end

Recursion issues

As we've already seen in the section about renaming-issues recursive formals can add quite a lot of complexity to the language.

Let's again have a look at this simple example:

class TEST[G -> H, H -> G]
end

A valid generic derivation for this example has the property, that both formals have to be exactly the same type. Otherwise it's impossible to meet the constraints. The conclusion is, that recursion has no practical benefit for the developer. One can however define certain things more general and maybe mathematically more consistent. But as constraints are to a formal, what inheritance is to a class, it seems also consistent to disallow cycles for formals as well. As a cycle in the inheritance hierarchy is indeed invalid.