EiffelBase2

Overview

EiffelBase2 is a general-purpose data structures library for Eiffel. It is intended as the future replacement for the EiffelBase library, which has for many years played a central role in Eiffel development.

Download

You can download a stable release of EiffelBase2 from the downloads page: http://eiffelbase2.origo.ethz.ch/download

The latest version of the EiffelBase2 source code is available in the repository: https://svn.origo.ethz.ch/eiffelbase2/trunk/

Goals

The design goals for EiffelBase2 are:

• Verifiability. The library is designed to allow proofs of correctness.

• Complete specifications. Partly as a result of the verifiability goal, but also for clarity and documentation, the contracts associated with classes and features should describe the relevant semantics in its entirety.

• Simple and consistent hierarchy, in particular avoidance of descendant hiding and of "taxomania" (classes not representing a meaningful abstraction, unnecessary inheritance links).

Design

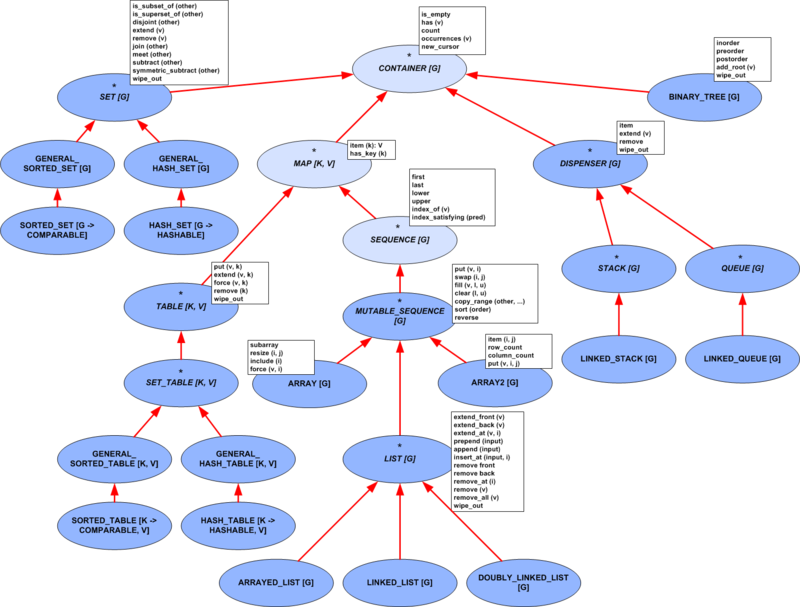
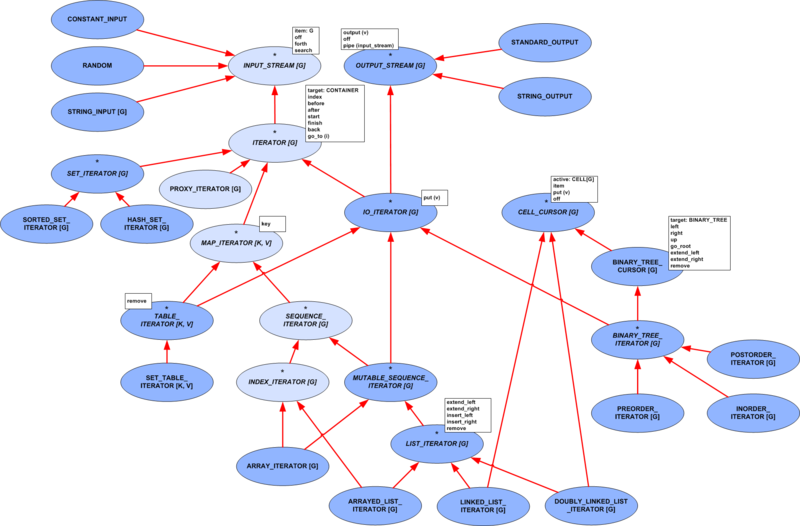
On the top level EiffelBase2 differentiates between containers and interfaces to access elements of containers, called accessors. A container is a finite storage of values. Accessors are either maps (accessing elements by a unique key) or streams (linear access). An observer is not necessarily bound to a container, e.g. RANDOM stream observes an infinite sequence of pseudo-random numbers. Streams that traverse containers are called iterators.

Below you can find the class diagram of EiffelBase2, split into two hierarchies. The first one is a hierarchy of containers and maps. All EiffelBase2 class names start with V_ (for Verified), but the prefix is omitted in the current document for brevity.

Container class hierarchy

The second one is a hierarchy of streams and iterators.

Iterator class hierarchy

Usage examples

Iterators

Here is how you can iterate through any container:

do_something (container: V_CONTAINER [INTEGER])
    local
        i: V_INPUT_ITERATOR [INTEGER]
    do
        from
            i := container.new_iterator
        until
            i.after
        loop
            print (i.item)
            i.forth
        end
    end

Here is some more advanced stuff you can do with lists:

do_something (list: V_LIST [INTEGER])
    local
        i: V_LIST_ITERATOR [INTEGER]
    do
        -- Find the last 0 at or before position 5:
        list.at (5).search_back (0)
        -- Find the first positive element at or after position 5:
        i := list.at (5)
        i.satisfy_forth (agent (x: INTEGER): BOOLEAN do Result := x > 0 end)
        -- And insert a 0 after it:
        i.extend_right (0)
    end

Sets and tables

Here is how you create and use a simple has table (keys must inherit from HASHABLE):

do_something
    local
        table: V_HASH_TABLE [STRING, INTEGER]
    do
        create table.with_object_equality
        table ["cat"] := 1
        table ["dog"] := 2
        print (table ["cat"] + table ["dog"])
        -- Prints "3"
    end

If you need a custom hash function or equivalence relation on keys, you can use V_GENERAL_HASH_TABLE, for example:

do_something
    local
        table: V_GENERAL_HASH_TABLE [STRING, INTEGER]
    do
        -- Create case-insensitive table:
        create table.make (
            agent {STRING}.is_case_insensitive_equal,
            agent (s: STRING): INTEGER do Result := s.as_lower.hash_code end
        )
        table ["cat"] := 1
        table ["dog"] := 2
        print (table ["CAT"] + table ["dog"])
        -- Prints "3"
    end

Similar style applies to V_HASH_SET and V_GENERAL_HASH_SET, V_SORTED_TABLE and V_GENERAL_SORTED_TABLE, V_SORTED_SET and V_GENERAL_SORTED_SET.

Stream piping

Iterators in EiffelBase2 are a special case of streams. Sometimes you can avoid writing a loop by piping an input stream into an output stream, for example:

do_something
    local
        array: V_ARRAY [INTEGER]
    do
        create array.make (1, 10)
        -- Fill array with random integers:
        array.at_first.pipe (create {V_RANDOM})
        -- Fill array with values parsed from a string:
        array.at_first.pipe (create {V_STRING_INPUT [INTEGER]}.make ("1 2 3 4 5 6 7 8 9 10", agent {STRING}.to_integer))
        -- Print array elements into standard output:
        (create {V_STANDARD_OUTPUT}).pipe (array.at_first)
        -- Prints "1 2 3 4 5 6 7 8 9 10 "
    end

Model-based contracts

Models

EiffelBase2 is specified using the model-based contracts specification method. This method prescribes that each class defines a model - a mathematical object that represents explicitly its abstract state space. The model of a class is expressed as tuple of one or more predefined mathematical objects: booleans, integers, sets, relations, maps, sequences or bags. We also introduce a special mathematical sort for object IDs (references).

Such mathematical objects in the program are represented by model classes, which are immutable and thus are straightforward translations of mathematical definitions. The Mathematical Model Library (MML), which is a part of EiffelBase2 contains model classes for sets, relations, maps, sequences and bags. Boolean and integer components of models are represented by standard classes BOOLEAN and INTEGER. Finally, arbitrary reference classes can be used as model components to denote the mathematical sort of references.

For example, a mathematical sequence is a model for a stack or a queue. A pair consisting of a sequence and an integer is a model for a list with an internal cursor.

The value of each component of the model is defined by a model query. You define the model of the class in the source code by listing its model queries under the tag model in the class's note clause. For example:

note
    model: sequence, index
class LIST [G]
feature -- Access
    index: INTEGER
            -- Cursor position
        deferred
        end
...
feature -- Specification
    sequence: MML_SEQUENCE [G]
            -- Sequence of list elements
        note
            status: specification
        ...
end

Here we declared the model of class LIST consisting of two components: a mathematical sequence of type MML_SEQUENCE and an integer index. As you can see, model queries are not necessarily introduced specifically for specification purposes (as is the case with sequence); regular queries meant to be called from the code can be also reused as model queries (as index in this example). We attach a status: specification note to a query to indicate that its primary purpose is specification.

Contracts

The purpose of introducing model queries is to define the postconditions of the regular features in their terms. For queries we define their result (or the model of the result, in case the query returns a fresh object) as a function of the model of Current and (the models of) the arguments. Definitions of zero-argument queries, as usual, can be moved to the class invariant. For commands we define their effects on the model queries of Current and the arguments. If a model query is not mentioned in the postcondition of a command, it is equivalent to stating that it's not modified.

The model-based contracts approach does not constrain the way in which you write preconditions: it is not necessary to express them through model queries if they can be conveniently expressed otherwise.

Class invariants in the model-based contracts approach constrain the values of model queries to make them reflect precisely the abstract state space of the class.

Let us add a couple of features and model-based contracts into the class LIST shown above:

note
    model: sequence, index
class LIST [G]
 
feature -- Access
    item: G
            -- Item at current position
        require
            not_off: not off
        deferred
        ensure
            definition: Result = sequence [index]
        end
...
 
feature -- Status report
    off: BOOLEAN
            -- Is cursor off all elements?
        deferred
        ensure
            definition: not sequence.domain [index]
        end
...
 
feature -- Element change
    put_right (v: G)
            -- Put `v' to the right of the cursor
        require
            not_after: not after
        deferred
        ensure
            sequence_effect: sequence |=| old (sequence.front (index).extended (v) + sequence.tail (index + 1))
            index_effect: index = old index
        end
...
 
invariant
    index_in_range: 0 <= index and index <= sequence.count + 1
end

Inheritance

If a class B inherits from A it is free to choose, whether to reuse each of A's model queries to represent its own model, as well as introduce new model queries. If B does not reuse an A's model query is has to provide a linking invariant: a definition of the old model query in terms of B's model. Linking invariants explain the parent's model in terms of the heir's model and thus make sure that the inherited model-based contracts make sense in the heir.

For example, suppose that LIST inherits directly from CONTAINER, whose model is a bag:

note
    model: bag
class CONTAINER [G]
...
end
 
note
    model: sequence, index
class LIST [G]
...
invariant
    ...
    bag_domain_definition: bag.domain = sequence.range
    bag_definition: bag.domain.for all (agent (x: G): BOOLEAN
        do Result := bag [x] = sequence.occurrences (x) end)
end

Here the linking invariant, provided as part of the class invariant in LIST completely defines an old model query bag in terms of a new model query sequence.

Status and roadmap

EiffelBase2 is currently being developed as a project at ETH Zurich.

ToDo list

• Add immutable and mutable strings.
• Make model class implementation more efficient.
• Add classes and directories.
• Rewrite loops using the across where appropriate.
• Add an iterator over keys for TABLE.
• Make the library void-safe.
• Implement more efficient data structures: e.g., tables with fast lookup both ways, heaps, skip lists, treaps, etc.